升研教育考研频道为23考研、24考研的同学们整理了“考研高数：微分中值定理”的相关信息，希望对正在备考的你有所帮助。考研复习效率不高怎么办？自己备考抓不住重点？想报考985/211等热门院校，但是没把握？升研教育推出考研集训营，全日制封闭式面授，10余年授课经验的老师，浓厚的学习氛围助你冲击目标、一战上研！

微分中值定理

一、罗尔定理

设函数f(x)满足

(1)在闭区间[a,b]上连续;

(2)在开区间(a,b )内可导;

(3) f(a)= f(b)

则存在ξ∈(a,b)，使得f'(ξ)=0

几何意义:

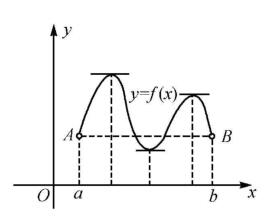
条件(1)说明:曲线y= f(x)在A(a, f(a))和B(b, f(b))之间是连续曲线;[包括点A和点B]。

条件(2)说明:曲线y= f(x)在A, B之间是光滑曲线，也即每一点都有不垂直于x轴的切线[不包括点A和点B]。

条件(3)说明:曲线y= f(x)在端点A和B处纵坐标相等。

结论说明曲线y= f(x)在点A和点B之间[不包括点A和点B ]至少有一点，它的切线平行于x轴。

例题：

二、拉格朗日中值定理

设函数f(x)满足

(1)在闭区间[a,b]上连续;

(2)在开区间(a,b)内可导，则存在ξ∈(a,b)，使得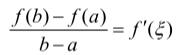或写成f(b)- f(a)=f"(ξ)(b-a) (a<ξ<b)，有时也写成f(x₀+Δx)- f(x₀)= f'(x₀+ θΔx).Δx (0<θ<1)这里x₀相当a或b都可以，Δx 可正可负。

几何意义:

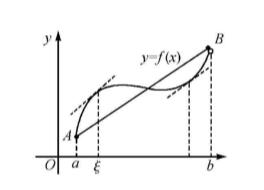
条件(1)说明:曲线y= f(x)在点A(a, f(a))和点B(b, f(b))之间[包括点A和点B ]是连续曲线

条件(2) 说明:曲线y= f(x)[不包括点A和点B ]是光滑曲线。

结论说明:曲线y= f(x)在A，B之间[不包括点A和点B],至少有点，它的切线与割线AB是平行的。

推论1若f(x)在(a,b)内可导，且f"(x)=0，则f(x)在(a, b)内为常数。

推论2若f(x)和g(x)在( a,b )内可导，且f"(x)= g(x;，则在(a,b)内f(x)=g(x)+C，其中C为一个常数。

(注:拉格朗日中值定理为罗尔定理的推广，当f(a)= f(b)特殊情形，就是罗尔定理)

例题：

三、柯西中值定理

设函数f(x)和g(x)满足:

(1)在闭区间[a，b ]上皆连续;

(2)在开区间(a，b )内皆可导;且g'(x)≠0， 则存在ξ∈(a, b)使得

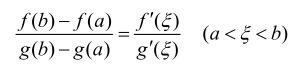
(注:柯西中值定理为拉格朗日中值定理的推广，特殊情形g(x)=x时，柯西中值定理就是拉格朗日中值定理)

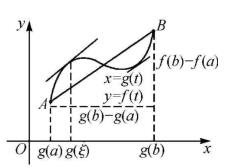
几何意义:考虑曲线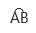的参数方程

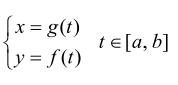
点A(g(a), f(a))，点B(g(b), f(b))曲线在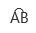上是连续曲线，除端点外是光滑曲线，那么在曲线上至少有一点，它的切线平行于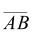值得注意:在数学理论上，拉格朗日中值定理最重要，有时也称为微分学基本定理。罗尔定理看作格朗日中值定理的预备定理，柯西中值定理虽然更广，但用得不太多。在考研数学命题中，用罗尔定理最多，其次是用拉格朗日中值定理，而用柯西中值定理也是较少。

四、泰勒定理(泰勒公式)

定理1 (带皮亚诺余项的n阶泰勒公式)

设f(x)在x₀处有n阶导数，则有公式

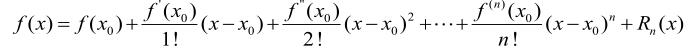
(x→x₀),其中R_n(x)=ο[(x-x₀)"] (x→x_o)称为皮亚诺余项。

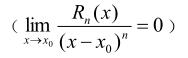
定理2:(带拉格朗日余项的n阶泰勒公式)

设f(x)在包含x₀的区间(a,b)内有n+1阶导数，在[a,b] 上有n阶连续导数，则对x∈[a,b]，有公式

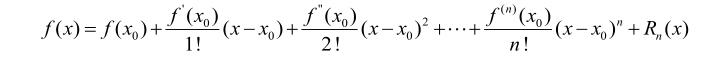
其中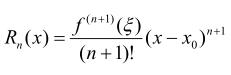(ξ在x₀与x之间)称为拉格朗日余项。

上面展开式称为以x₀为中心的n阶泰勒公式。x₀= 0时，也称为麦克劳林公式。

如果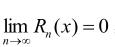那么泰勒公式就转化为泰勒级数，这在后面无穷级数中再讨论。

例题：